Pilgrimage To Logicavan Math

If your math skills are approximated above, the following logic may be unattainable. I had some trouble with it myself, but I am amused by the concept:

"Every year I get a few kids in my classes who argue with me on this. And there are arguers all over the web. And I just know I'm going to get contentious "but it just can't be true" whiners in my comments. But I feel obliged to step into this fray.

.9 repeating equals one. In other words, .9999999... is the same number as 1. They're 2 different ways of writing the same number. Kind of like 1.5, 1 1/2, 3/2, and 99/66. All the same. I know some of you still don't believe me, so let me say it loudly:

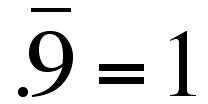
Do you believe it yet? Well, I do have a couple of arguments besides mere size. Let's look at some reasons why it's true. Then we'll look at some reasons why it's not false, which is something different entirely. The standard algebra proof (which, if you modify it a little, works to convert any repeating decimal into a fraction) runs something like this. Let x = .9999999..., and then multiply both sides by 10, so you get 10x = 9.9999999... because multiplying by 10 just moves the decimal point to the right. Then stack those two equations and subtract them (this is a legal move because you're subtracting the same quantity from the left side, where it's called x, as from the right, where it's called .9999999..., but they're the same because they're equal. We said so, remember?):

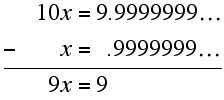
Surely if 9x = 9, then x = 1. But since x also equals .9999999... we get that .9999999... = 1. The algebra is impeccable.

But I know that this is unconvincing to many people. So here's another argument..."

For more arguments, and attempts at refutation, go to:

Polymathematics: No, I'm sorry, it is

Personally, I'm still struggling with the idea that you can't divide by zero.